
Fallacy of exclusive premises (eng) (izvor: wikipedia)
Greška uzajamno isključive premise je poznata i pod imenom Greška odričnih premisa (eng: Fallacy of Two Negative Premises).
Uzajamno isključive premise je logička greška koja nastaje kada su obe premise odrične, jer se iz takvih premisa ne može izvući validan zaključak. Neophodno je da barem jedna od premisa bude potvrdna.
Oblik:
Premisa 1: Nijedan A nije B.
Premisa 2: Neki B nisu C.
Zaključak: Dakle, neki C nisu A.
Iz datih premisa se ne može zaključiti da neki C obavezno nisu A, možda su svi C ujedno i A.
Primer 1:
Premisa 1: Nijedna životinja nije insekt.
Premisa 2: Neki insekti nisu psi.
Zaključak: Dakle, neki psi nisu životinje.
Iz ovog primera se jasno vidi da negde postoji problem, pošto znamo da su svi psi životinje. Problem je upravo u odričnim premisama.
Ne smemo zaboraviti da zaključak pogrešnog argumenta, logičke greške, može biti istinit, ali je sam argument i dalje pogrešan ako zaključak nikako logički ne sledi iz datih premisa.
Primer 2:
Premisa 1: Nijedan nilski konj nije profesionalni bokser.
Premisa 2: Neki profesionalni bokseri nisu katolici.
Zaključak: Dakle, neki katolici nisu nilski konji.
Ovde vidimo da je zaključak istinit jer zaista ima katolika koji nisu nilski konji, ali je sam argument i dalje pogrešan jer se takav zaključak ne može izvesti iz zadatih premisa.
Primer 3:
Premisa 1: Nijedan Sicilijanac nije Japanac.
Premisa 2: Nijedan Japanac nije Italijan.
Zaključak: Dakle, nijedan Sicilijanac nije Italijan.
Iako zaključak izgleda validno, znamo da nije jer su skoro svi Sicilijanci ujedno i Italijani.
Uzajamno isključive premise je greška zbog toga što svaki argument mora da sadrži barem jednu potvrdnu premisu, u protivnom nemamo nikakve informacije iz kojih bismo mogli da izvučemo validan zaključak. Odrične premise govore samo o tome šta nešto nije, a da bismo imali mogućnost da izvučemo bilo kakav validan zaključak neophodno je da imamo barem jednu informaciju o tome šta nešto jeste.

Negative conclusion from affirmative premises (eng) (izvor: wikipedia)
Negativan zaključak iz potvrdne premise je logička greška koja nastaje kada se odričan zaključak izvuče iz dve potvrdne premise.
Postoje dva oblika ove greške.
Oblik 1:
Premisa 1: Neki A su B.
Premisa 2: Neki B su C.
Zaključak: Dakle, neki A nisu C.
Iz datih premisa se ne može zaključiti da neki A obavezno nisu C, možda su svi A ujedno i C.
Oblik 2:
Premisa 1: Neki A su B.
Premisa 2: Neki B su C.
Zaključak: Dakle, nijedan A nije C.
Iz datih premisa se ne može zaključiti nijedan A nije C, možda je neki od B, koji je ujedno i A, dodatno i C.
Odričan zaključak iz potvrdnih premisa je greška zbog toga što svaki argument koji sadrži samo potvrdne premise mora i sam biti potvrdan.

Affirmative conclusion from a negative premise (eng) (izvor: wikipedia)
Potvrdan zaključak iz odrične premise je logička greška koja nastaje kada se potvrdan zaključak izvuče iz jedne ili više odričnih premisa.
Primer 1:
Premisa 1: Ribe nisu psi.
Premisa 2: Psi ne mogu da lete.
Zaključak: Dakle, ribe mogu da lete.
Iz datih premisa se ne može zaključiti da li ribe mogu da lete ili ne.
Primer 2:
Premisa 1: Mi ne čitamo takvo đubre.
Premisa 2: Ljudi koji čitaju takvo đubre ne vrednuju pravu literaturu.
Zaključak: Dakle, mi vrednujemo pravu literaturu.
Iz datih premisa se ne može zaključiti da li mi vrednujemo pravu literaturu ili ne.
Ovo se matematički može prikazati uz pomoć skupova:
Ako je A ∩ B = ∅ i B ∩ C = ∅, onda je A ⊂ C.
Ili rečima: Ako je presek A i B prazan skup i presek B i C prazan skup, onda je A podskup skupa C.
Potvrdan zaključak iz odrične premise je greška zbog toga što svaki argument koji sadrži barem jednu odričnu premisu mora imati i odričan zaključak da bi bio validan.

Broken compass argument (eng) (izvor: ironchariots)
Pokvareni kompas je logička greška koja nastaje kada iz jedne premise sledi više različitih, često potpuno isključujućih, zaključaka.
Na primer:
Premisa 1: Molitva je način spoznaje boga.
Premisa 2: Ja sam se molio i spoznao boga.
Zaključak: Dakle, taj moj bog postoji.
Problem sa ovim argumentom je što ga mogu primeniti pripadnici bilo koje religije, pa je stoga “validan” za hrišćanskog boga isto kao i za muslimanskog, ili jevrejskog ili nekog od nordijskih bogova, ili starogrčkih i tako dalje, ad infinitum.
Naziv ove logičke greške potiče od činjenice da će se kompas koji radi sam ispraviti ako se okrene, dok će pokvareni kompas pokazivati sever jednako u svim pravcima. Isto tako, logička greška pokvareni kompas upućuje na različite strane, zaključke, u zavisnosti od toga kako je korišćen.
Pokvareni kompas je podvrsta logičke greške ne sledi (lat. non sequitur). Logičke greške argument iz vere, iz tradicije, iz većine, iz autoriteta ili pozivanje na emocije su sve u osnovi verzije logičke greške pokvareni kompas.
Argumenti koji se baziraju na razumu se samoispravljaju baš kao i kompas koji radi, za razliku od svih nabrojanih logičkih grešaka.

The Existential Fallacy (eng)
Egzistencijalna zabluda je logička greška koja nastaje kada zaključak implicira da postoji barem jedan član određene grupe, iako premise to ne podržavaju. Ovo se najčešće dešava kada se iz opštih premisa izvuče specifičan zaključak.
Primer:
Premisa: Svi jednorozi su životinje.
Zaključak: Dakle, neke životinje su jednorozi.
Nisu.
Problem je, kao što se vidi, u činjenici da se pretpostavlja da su premise istinite, a u stvari to što one pretpostavljaju da obavezno postoji u stvari ne postoji (egzistencija).
Drugim rečima, u primeru se pretpostavlja da postoje jednorozi.

Denying the antecedent (eng)
Inverzna zabluda je logička greška koja nastaje kada se izvede zaključak da je inverzija osnovne postavke obavezno tačna.
Generalni oblik ove greške je:
Premisa 1: Ako P, onda Q.
Premisa 2: Nije P.
Zaključak: Dakle, nije Q.
Argument u ovakvom obliku je pogrešan, zato što zaključak može biti neistinit čak i ako su obe premise istinite. U prvoj premisi nigde nije naznačeno da je P ujedno i jedini neophodan uslov za Q. Drugi faktori mogu dovesti do Q (čak i kada je P neistinito).
Drugim rečima, ako P obavezno implicira Q, kao što prva premisa kaže, onda jedino što možemo da zaključimo je da ne-Q implicira ne-P. (ne-P i ne-Q označavaju suprotne izjave od P i Q)
Ovo se zove logički kontrapozitiv:
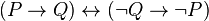
Ali nikako ne možemo da zaključimo i da ne-P obavezno implicira ne-Q.
Primeri:
Premisa 1: Ako je Rene Dekart razmišljao, onda je Rene Dekart postojao.
Premisa 2: Jednom se dogodilo da Rene Dekart nije razmišljao.
Zaključak: Dakle, Rene Dekart tada nije postojao.
Nerazmišljanje Dekarta nigde nije postavljeno kao uslov za njegovo nepostojanje. Drugim rečima, veza između razmišljanja i postojanja ide samo u jednom pravcu. Razmišljanje znači postojanje ali nerazmišljanje ne znači nepostojanje.
Sa druge strane, možemo sa sigurnošću da zaključimo da ako Rene Dekart ne postoji (ne-Q) onda je sigurno tačno da Rene Dekart ne razmišlja (ne-P). Ovo je kontrapozitiv prve premise i mora biti istinit ako je prva premisa istinita.
Premisa 1: Ako je Elizabeta II američka državljanka, onda je Elizabeta II ljudsko biće.
Premisa 2: Elizabeta II nije američka državljanka.
Zaključak: Dakle, Elizabeta II nije ljudsko biće.
Ovaj argument je više nego očigledno pogrešan. Ali je ipak odličan primer logičke greške inverzna zabluda.
Argumenti u ovom obliku ipak mogu izgledati površno uverljivo i zato je neophodno da ovu grešku dobro poznajemo.

Affirming the consequent (eng)
Potvrđivanje suprotnosti je logička greška koja nastaje kada se određena postojeća uzročno posledična veza obrne i kada se tvrdi da je suprotna uzročno posledična veza istinita.
Generalni oblik ove greške je:
Premisa 1: Ako P, onda Q.
Premisa 2: Q.
Zaključak: Dakle, P.
Argument u ovakvom obliku je pogrešan, zato što zaključak može biti neistinit čak i ako su obe premise istinite. U prvoj premisi nigde nije naznačeno da je P ujedno i jedini neophodan uslov za Q. Drugi faktori mogu dovesti do Q (čak i kada je P neistinito).
Drugim rečima, ako P obavezno implicira Q, kao što prva premisa kaže, onda jedino što možemo da zaključimo je da ne-Q implicira ne-P. (ne-P i ne-Q označavaju suprotne izjave od P i Q)
Ovo se zove logički kontrapozitiv:
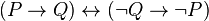
Ali ne možemo da zaključimo i da Q obavezno implicira P.
Primeri:
Premisa 1: Ako Bil Gejts poseduje Fort Noks, onda je on bogat.
Premisa 2: Bil Gejts je bogat.
Zaključak: Dakle, Bil Gejts poseduje Fort Noks.
Posedovanje Fort Noksa nije jedini uslov da bi neko bio bogat.
Postoji veliki broj drugih načina da neko bude bogat.
Sa druge strane, možemo sa sigurnošću da zaključimo da ako Bil Gejts nije bogat (ne-Q), onda je sigurno tačno da Bil Gejts ne poseduje Fort Noks (ne-P). Ovo je kontrapozitiv prve premise i mora biti istinit ako je prva premisa istinita.
Premisa 1: Ako sam oboleo od gripa, boli me grlo.
Premisa 2: Boli me grlo.
Zaključak: Dakle, oboleo sam od gripa.
Ali grip nije jedini uzrok bola u grlu.
Možda je u pitanju obična prehlada ili streptokokna upala grla.

Affirming a disjunct (eng)
Zabluda lažno isključivo razdvajanje je logička greška koja nastaje kada se dve opcije koje nisu međusobno isključive, predstave kao moguće opcije i zatim se na osnovu istinitosti jedne opcije zaključi da druga nije istinita. Greška je upravo zbog toga što je moguće da obe opcije budu istovremeno istinite.
Primeri:
Premisa 1: Ići ću u krevet ili ću gledati TV.
Premisa 2: Dosta sam umoran, pa ću ipak leći u krevet.
Zaključak: Dakle, neću gledati TV.
Ujedno je i logički a fizički sasvim moguće ležati u krevetu i gledati TV. Znam to sigurno jer upravo to radim skoro svakog dana. Ponuđeno razdvajanje u prvoj premisi ne isključuje tu opciju.
Premisa 1: Ptica je živa ili je na zemlji.
Premisa 2: Ptica je na zemlji.
Zaključak: Dakle, ptica nije živa.
Kao i u prethodnom primeru, sasvim je moguće da živa ptica bude na zemlji.
Primer ispravnog razdvajanja:
Premisa 1: Danas je subota ili nedelja.
Premisa 2: Danas je nedelja.
Zaključak: Dakle, danas nije subota.

Masked man fallacy (eng)
Zabluda maskiranog čoveka je logička greška koja nastaje kada se u argumentu pogrešno upotrebi Lajbnicov zakon, koji kaže da ako jedan objekat ima odeređenu osobinu, dok drugi objekat nema tu istu osobinu, onda ta dva objekta ne mogu biti identična.
Naziv ove greške dolazi iz primera:
Premisa 1: Ja znam ko je Jovan.
Premisa 2: Ja ne znam ko je maskirani čovek.
Zaključak: Dakle, Jovan nije maskirani čovek.
Premise mogu biti istinite i zaključak pogrešan ako Jovan zaista jeste maskirani čovek ali govornik to jednostavno ne zna. Zbog toga je ovakav argument pogrešan.
Još jedan primer:
Premisa 1: Luis zna da supermen može da leti.
Premisa 2: Luis ne veruje da Klark Kent može da leti.
Zaključak: Dakle, Supermen i Klark Kent nisu ista osoba.
U ovom primeru je problem to što se nešto u šta Luis veruje/ne veruje uzima kao da je objektivna činjenica, a nije.
Ali, ako malo promenimo prvi primer, dobićemo potpuno validan i ispravan argument:
Premisa 1: Ja znam ko je Jovan.
Premisa 2: Maskirani čovek definitivno nije neko koga ja poznajem.
Zaključak: Dakle, Jovan nije maskirani čovek.

Base rate fallacy (eng)
Zanemarivanje osnovne stope je logička greška koja nastaje kada se prilikom analize generalne verovatnoće i neke specifične verovatnoće, zanemaruje generalna verovatnoća i fokus u prebacuje na specifičnu verovatnoću.
Ova greška nastaje kada se veći značaj pridaje specifičnim informacijama nego što bi trebalo, a ponekad se osnovne, generalne informacije čak u potpunosti ignorišu. Većina događaja imaju generalnu verovatnoću, ili osnovnu stopu – od muževa koji varaju pa do pasa koji imaju neku bolest – moguće je izračunati generalnu verovatnoću ovih događaja. Ali, kada je u pitanju moj pas, postoji određena pristrasnost koja me navodi da zanemarim generalnu verovatnoću i fokusiram se samo na specifične podatke o tom mom psu.
Primer:
Jovan je muškarac koji nosi gotsku odeći, ima dugačku crnu kosu i sluša death metal. Kolika je verovatnoća da je on hrišćanin a kolika da je satanista?
Ljudi će uvek drastično umanjiti verovatnoću da je Jovan hrišćanin, a isto tako drastično povećati verovatnoću da je satanista. Ovo se događa zato što se zanemaruje verovatnoća da je hrišćanin (kojih ima oko 2 milijarde), koja je drastično veća od verovatnoće da je satanista (kojih ima samo par hiljada). Dakle, čak i ako Jovanov izbor odeće ukazuje na skok reda veličine verovatnoće da je satanista, i dalje je verovatnoća da je hrišćanin značajno veća.
Primer:
Policija ima alkotest aparate koji u 5% slučajeva treznih ljudi pokazuju pogrešno da su pijani. Sa druge strane su 100% tačni kada je u pitanju zaista pijana osoba. Dodatno znamo da je 1 na svakih 1000 vozača u pijanom stanju. Pretpostavimo, onda, da policija nasumično zaustavi jednog vozača i alkotest pokaže da je u pijanom stanju. Kolika je verovatnoća da je on/ona zaista u pijanom stanju?
Mnogi će reći da je verovatnoća velika, možda će čak i dati broj od 95%. Međutim, tačan odgovor je 2% šanse da je zaustavljena osoba zaista u pijanom stanju.
Rešenje je prosto. Zamislimo da su policajci testirali 1000 vozača. 1 je sigurno pijan i za njega je rezultat 100% tačan. Ostalih 999 su trezni a 5% njih je dobilo pogrešan rezultat da jesu u pijanom stanju. To je 49.95 ljudi, zaokružimo na 49. Dakle, od 50 ljudi koji su dobili rezultat da su pijani, samo 1 od njih zaista i jeste pijan. Dakle, samo 2%.
Zanimljivo je da ako se problem samo malo drugačije prezentuje, ljudi tada imaju tendenciju da daju odgovor koji je mnogo bliži tačnom odgovoru:
Policija ima alkotest aparate koji nikada ne greši kada se testira zaista pijana osoba. Za 50 od 999 treznih osoba, alkotest aparati pogrešno kažu da su pijani. Pretpostavimo, onda, da policija nasumično zaustavi jednog vozača i alkotest pokaže da je u pijanom stanju. Kolika je verovatnoća da je on/ona zaista u pijanom stanju?
Takođe je primećeno da grafički prikaz informacija takođe pomaže ljudima da daju ispravan odgovor.

